


Next: Polarization efficiency: size/shape/orientation effects
Up: Optical properties of cosmic
Previous: The 2175Å feature
Polarization properties (transmitted radiation)
To model the interstellar polarization one needs to calculate the forward-transmitted
radiation for an ensemble of non-spherical aligned dust grains.
This procedure consists of two steps:
1) computations of the extinction cross-sections for two polarization modes and
2) averaging of cross-sections for given
particles size and orientation distributions.
Although the average cross-sections
should be compared with observations,
behaviour of the polarization cross-sections and alignment mechanisms
are often analysed separately.
Let non-polarized stellar radiation passes through a dusty cloud
with a homogeneous magnetic field. As follows from observations and
theoretical considerations (Dolginov et al., [1979]),
the magnetic field determines the direction of alignment of dust grains.
The angle between the line of sight and the magnetic field is
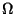 (
(
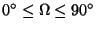 ).
The linear polarization
produced by a rotating spheroidal particle
of same size is
).
The linear polarization
produced by a rotating spheroidal particle
of same size is
where
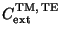 are the extinction cross-sections
for two polarization modes (Sect.
are the extinction cross-sections
for two polarization modes (Sect. ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ),
),
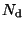 the column density of dust grains.
The particles are assumed to be partially aligned:
the major axis of the particle rotates in the spinning plane
(
the column density of dust grains.
The particles are assumed to be partially aligned:
the major axis of the particle rotates in the spinning plane
(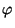 is the spin angle) which is perpendicular to the angular
momentum
is the spin angle) which is perpendicular to the angular
momentum 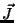 .
. 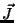 spins (precesses) around the direction ofmagnetic field (
spins (precesses) around the direction ofmagnetic field (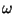 is the precession angle),
is the precession angle),
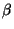 is the precession-cone angle for
is the precession-cone angle for 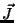 .
This is the imperfect Davies-Greenstein
(IDG) orientation described by the function
.
This is the imperfect Davies-Greenstein
(IDG) orientation described by the function
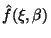 which depends on the alignment parameter
which depends on the alignment parameter 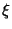 and
the angle
and
the angle 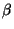 .
.
Note that the problem of grain alignment is one
of the most difficult in the physics
of cosmic dust. Here, the interaction of solid particles with
gas, radiation and magnetic field is closely connected.
Davies and Greenstein ([1951]) assumed that
Fe atoms embedded in dielectric particles gave them paramagnetic
properties and opened the possibility of interaction with a weak
interstellar magnetic field.
The required orientation arises as a result of the
effect of paramagnetic relaxation of thermally rotating
grains.
The Davies-Greenstein mechanism was further developed by Jones and Spitzer ([1967])
who obtained expressions for the distribution of
angular momentum. In the simplest case, it is
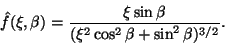 |
(8) |
The parameter 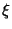 is a function of the
particle size
is a function of the
particle size 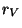 , the imaginary part of the grain magnetic susceptibility
, the imaginary part of the grain magnetic susceptibility
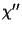 (
(
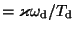 , where
, where
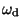 is the angular velocity
of grain), gas density
is the angular velocity
of grain), gas density 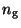 , the strength of magnetic field
, the strength of magnetic field 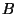 and dust (
and dust (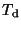 ) and gas (
) and gas (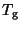 ) temperatures
) temperatures
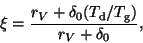 |
(9) |
where
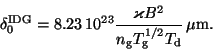 |
(10) |
The angle 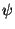 in Eq. (8) is expressed
via the angles
in Eq. (8) is expressed
via the angles
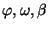 and
and
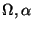 (for definitions of the angles and relations between them see, for example,
Hong and Greenberg, [1980] or Voshchinnikov, [1989]).
(for definitions of the angles and relations between them see, for example,
Hong and Greenberg, [1980] or Voshchinnikov, [1989]).
Rotation is an important factor of any grain alignment mechanism.
The faster it is the more effective the grain alignment should be.
The Davies-Greenstein mechanism considers thermally rotating
grains. Purcell ([1979]) suggested a mechanism
of supra-thermal spin alignment
(SSA; ``pinwheel'' mechanism)
where the grains were spun up to very high velocities
as a result of the desorption of H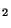 molecules from their surfaces.
In this case, the alignment function is described by
Eq. (9) but the parameter
molecules from their surfaces.
In this case, the alignment function is described by
Eq. (9) but the parameter 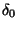 is
is
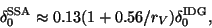 |
(11) |
where 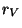 is in
is in 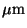 .
Rotation can also arise due to radiation torques when ``helical''
grains scatter left- and right-circularly
polarized light in a different way
(Dolginov et al., [1979]; Draine and Weingartner, [1996],
[1997]), which can lead to the grain alignment in anisotropic
radiation field. Alignment of thermally rotating grains is also
possible by supersonic flows or Alfvénic waves or ambipolar
diffusion. This so-called
Gold-type3 of
mechanical alignment
was generalized for supra-thermally rotating grains by Lazarian ([1995]).
Note that some mechanisms can produce alignment when the
major grain axes tend to align parallel to the magnetic field.
Such an orientation is ``wrong'' for interstellar polarization but
the mechanism may be ``right'' and
operate in other conditions, for example in jets from YSO.
.
Rotation can also arise due to radiation torques when ``helical''
grains scatter left- and right-circularly
polarized light in a different way
(Dolginov et al., [1979]; Draine and Weingartner, [1996],
[1997]), which can lead to the grain alignment in anisotropic
radiation field. Alignment of thermally rotating grains is also
possible by supersonic flows or Alfvénic waves or ambipolar
diffusion. This so-called
Gold-type3 of
mechanical alignment
was generalized for supra-thermally rotating grains by Lazarian ([1995]).
Note that some mechanisms can produce alignment when the
major grain axes tend to align parallel to the magnetic field.
Such an orientation is ``wrong'' for interstellar polarization but
the mechanism may be ``right'' and
operate in other conditions, for example in jets from YSO.
The development and current status of the major alignment mechanisms and principal
physical processes forming their basis are reviewed by
Roberge ([1996]),
Lazarian et al. ([1997]) and Lazarian ([2000]).
Unfortunately, the astrophysical significance of different alignment
mechanisms remains unclear. This is connected, in particular,
with very rough theoretical estimates of the
polarization efficiency when
instead of an alignment function like that given by Eq. (9)
the Rayleigh reduction factor (see Greenberg, [1968])
is used (e.g., Lazarian et al., [1997]).
The circular polarization is proportional to the product
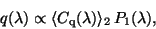 |
(12) |
where
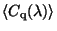 is the average cross-section of circular
polarization.
The cross-section
is the average cross-section of circular
polarization.
The cross-section
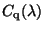 is calculated as
the difference of phase lags
is calculated as
the difference of phase lags
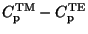 represented by the imaginary parts of the corresponding
complex extinction cross-sections.
The circular polarization arises when the radiation
linearly polarized in cloud ``1'' passes through cloud ``2''
(note the indices in Eq. (13)).
Cloud ``1'' works as a linear polarizer and
cloud ``2'' as a linear retarder.
In such an optical device, the maximum transformation
of the linear polarization to the circular one occurs when the
optical axes of components are inclined by 45
represented by the imaginary parts of the corresponding
complex extinction cross-sections.
The circular polarization arises when the radiation
linearly polarized in cloud ``1'' passes through cloud ``2''
(note the indices in Eq. (13)).
Cloud ``1'' works as a linear polarizer and
cloud ``2'' as a linear retarder.
In such an optical device, the maximum transformation
of the linear polarization to the circular one occurs when the
optical axes of components are inclined by 45
 (e.g., Tinbergen, [1996]).
(e.g., Tinbergen, [1996]).
For simplicity, non-rotating particles of the same orientation
are frequently considered. In this case of ``picket fence'' (PF)
orientation, there are no integrals over angles
 and
and  in Eq. (8).
The polarization degree is proportional to the polarization cross-section
in Eq. (8).
The polarization degree is proportional to the polarization cross-section
![$P(\lambda) \propto C_{\rm pol} =
1/2 [C^{\rm TM}_{\rm ext}(\Omega) -C^{\rm TE}_{\rm ext}(\Omega)]$](img141.gif) , where
, where
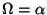 .
The dichroic polarization efficiency is defined
by the ratio of the polarization cross-section (factor) to the
extinction one
.
The dichroic polarization efficiency is defined
by the ratio of the polarization cross-section (factor) to the
extinction one
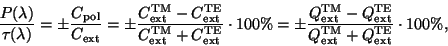 |
(13) |
where the upper (lower) sign is related to prolate (oblate) spheroids.
This ratio describes the efficiency of polarization of light
transmitted through an uniform slab consisting of non-rotating
particles of the same orientation.
A more complicated case is the perfect rotational (2D) orientation
(or perfect Davies-Greenstein orientation, PDG)
when the major axis of a non-spherical particle always lies in the same plane.
For the 2D orientation, integration is performed over the spin
angle 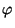 only.
This gives for prolate spheroids
only.
This gives for prolate spheroids
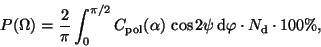 |
(14) |
where the angle 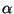 is connected with
is connected with 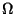 and
and 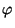 (
(
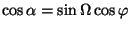 ). For oblate spheroids randomly aligned
in a plane, we have
). For oblate spheroids randomly aligned
in a plane, we have
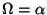 and
and
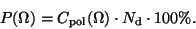 |
(15) |
As a result, the expected polarization will be determined by:
- the particle refractive index, size and shape via the polarization
cross-section
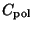 ;
;
- the relation between the strength of
the magnetic field, gas and dust
temperature, gas density, etc. via the alignment function
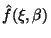 ;
;
- the direction of alignment depending on the angle
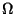 (or
(or 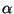 ) via both
) via both 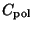 and
and
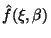 .
.
The simplest types of orientations like PF or
PDG allow
one to investigate the influence of the first and third factors.
The dependence of 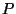 on
on 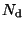 is excluded because
the normalized polarization or polarization efficiency is usually
studied.
is excluded because
the normalized polarization or polarization efficiency is usually
studied.
Subsections



Next: Polarization efficiency: size/shape/orientation effects
Up: Optical properties of cosmic
Previous: The 2175Å feature
root
2003-04-09
![]() (
(
![]() ).
The linear polarization
produced by a rotating spheroidal particle
of same size is
).
The linear polarization
produced by a rotating spheroidal particle
of same size is
![]() molecules from their surfaces.
In this case, the alignment function is described by
Eq. (9) but the parameter
molecules from their surfaces.
In this case, the alignment function is described by
Eq. (9) but the parameter ![]() is
is
![]() and
and ![]() in Eq. (8).
The polarization degree is proportional to the polarization cross-section
in Eq. (8).
The polarization degree is proportional to the polarization cross-section
![]() , where
, where
![]() .
The dichroic polarization efficiency is defined
by the ratio of the polarization cross-section (factor) to the
extinction one
.
The dichroic polarization efficiency is defined
by the ratio of the polarization cross-section (factor) to the
extinction one
![]() only.
This gives for prolate spheroids
only.
This gives for prolate spheroids