


Next: Extinction efficiencies: general behaviour
Up: Optical properties of cosmic
Previous: Optical properties of cosmic
It is now evident that observed interstellar extinction
cannot be explain
using particles of only one kind.
Therefore, three tendencies in the modelling of multi-component
dust mixtures are being developed.
- Several populations of compact
(usually spherical) grains are used.
Populations consist of different materials. The optical properties
are calculated from the Mie theory. Such an approach was used
many times for the interpretation of the interstellar extinction curves
(e.g., Mathis et al., [1977]; Zubko et al., [1996])
and the SEDs in spectra of stars and
YSOs (see Table 7 in Voshchinnikov [2002]). In the
case of circumstellar shells, the authors do not worry about the problem of cosmic
abundances and can apply multi-component mixtures
with varying fractional abundances at different distances
from an object. For example, Men'shchikov et al. ([1999])
chose a four-component mixture to explain
observations of the young star HL Tau.
The disadvantage of such an approach is the impossibility of
including the vacuum as a component.
- Several materials are mixed using one of the EMT's rules
and
then the Mie theory is applied
for calculations of the optical properties
of such ``composite''
particles. In this case, there exist many doubts on
the validity of employing the EMT for significant fractional
abundances of components
as is discussed in Sect. 2.1.4 in Voshchinnikov [2002].
- Inhomogeneous (composite) particles with layers or
inclusions from different materials or aggregate particles
are considered and light scattering computations are made
using the DDA, TMM
or simpler theory like the Mie theory
for
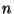 -layered spheres.
This approach seems to be the most promising because
it allows one to describe more exactly the properties of dust
grains.
However, calculations with the DDA are very time-consuming and
at the present
can be used rather for illustrative than for mass calculations (e.g.,
Wolff et al., [1994], Vaidya et al., [2001]).
The idea of composite particles as multi-layered spheres
(Voshchinnikov and Mathis, [1999];
see also Iatì et al., [2001]) looks
a bit artificial but attractive from the point of
view of numerical realization (see discussion in Sect. 1.1).
-layered spheres.
This approach seems to be the most promising because
it allows one to describe more exactly the properties of dust
grains.
However, calculations with the DDA are very time-consuming and
at the present
can be used rather for illustrative than for mass calculations (e.g.,
Wolff et al., [1994], Vaidya et al., [2001]).
The idea of composite particles as multi-layered spheres
(Voshchinnikov and Mathis, [1999];
see also Iatì et al., [2001]) looks
a bit artificial but attractive from the point of
view of numerical realization (see discussion in Sect. 1.1).
The intensity of radiation after passing a dust cloud 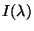 is equal to
is equal to
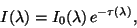 |
(1) |
where 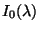 is the source (star) intensity and
is the source (star) intensity and 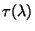 the optical thickness along the line of sight. The interstellar extinction is
the optical thickness along the line of sight. The interstellar extinction is
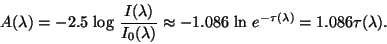 |
(2) |
Here, 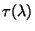 is the total extinction cross-section
of all type particles along the line of sight in given direction.
is the total extinction cross-section
of all type particles along the line of sight in given direction.
For spherical particles of radius  , we have
, we have
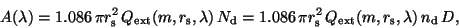 |
(3) |
where 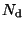 and
and 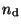 are the column and
number densities of dust grains, correspondingly and
are the column and
number densities of dust grains, correspondingly and 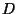 is the distance
to the star.
is the distance
to the star.
For a polydisperse ensemble, averaging over a size distribution should be performed
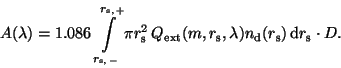 |
(4) |
Here,
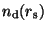 is the size distribution of dust grains with
the lower cut-off
is the size distribution of dust grains with
the lower cut-off 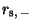 and the upper cut-off
and the upper cut-off  .
.
From Eqs. (3) and (4), the
important conclusion follows:
the wavelength dependence of interstellar extinction
is totally
determined by the wavelength dependence of the
extinction efficiencies 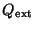 .
.
Subsections



Next: Extinction efficiencies: general behaviour
Up: Optical properties of cosmic
Previous: Optical properties of cosmic
root
2003-04-09
![]() is equal to
is equal to
![]() , we have
, we have
![]() .
.