I n t r o d u c t o r y n o t e s
The efficiency of interaction of radiation with a particle
and hence its optical properties depend on
the particle chemical composition, size, shape, structure, etc.
[1,2].
The optical constants characterizing the optical properties of
different materials are discussed in another
section of the DOP
while basic effects of the chemical composition (the refractive index)
on the optical properties are illustrated in our
graphics library.
Here we address other primary characteristics of scatterers.
Size.
Particle size expressed in units of the wavelength of
incident radiation, together with chemical composition,
most strongly affects the optical properties of a scatterer.
The simplest model that allows one to consider the influence
of size and composition variations is that of a homogeneous sphere.
The Mie theory is the solution to the light scattering from a sphere
and is applicable in the entire range of parameter values.
Note that the interaction of large molecules/very small grains (e.g.,
polycyclic aromatic hydrocarbons, PAH) with radiation is not described by
the macroscopic quantities and requires quantum mechanical
consideration [3].
Shape.
Real dust grains certainly differ from homogeneous spheres.
Deviations of their shapes from the spherical one can be of different
kinds - from small-scale surface fluctuations to large-scale shape defects.
The asphericity characterized by the ratio of the maximum to minimum
dimension of a scatterer looks to be most essential in astronomy
and some other fields and can be well modelled using spheroidal particles
as their shapes can vary from needles or disks to spheres.
Thus, the spheroidal model allows one to analyze
the effects of composition, size, and, to some extent, shape.
There are many methods to solve the light-scattering problem
for a homogeneous spheroid (our survey of the light-scattering
methods see here).
First among them should be mentioned
the separation of variables method (SVM) where
the wave equation is formulated
and the spheroidal wave functions are used in the solution
to expand the incident, internal and scattered fields.
Another popular approach - the extended boundary condition method
(EBCM) coupled with the T-matrix method (TMM)
consists of forming surface integral equation,
but utilizes the simpler spherical wave functions in the expansion.
For spheroids, the SVM and to a lesser degree the EBCM
conform more readily to the system geometries, and
as a result, the methods are much more fast and exact
than other (more universal) approaches like the discrete dipole
approximation (DDA) or finite difference time domain (FDTD)
method [2,4].
Note that medium scale defects of the scatterer surface (like cavities)
can be considered using the model of the Chebyshev particles and the EBCM
(see, e.g., [5] and references therein).
Scatterers with random surface fluctuations were studied, for instance,
in [6].
Structure.
Solid particles in real (e.g., cosmic) conditions hardly are homogeneous.
Their internal structures can include layers, large and small
(in comparison with the particle size) inclusions, and so on.
In principle, scatterers of any structure can be treated by
the methods using the representation of the scattering problem
in the form of volume integral equation (e.g., the widely used DDA).
The back sides of this universality are strong demands
for computer memory and speed which often make computations impossible.
Layered scatterers could be treated by the SVM and EBCM,
which would allow really extensive calculations,
but the theoretical methods are not yet well developed.
If the dimensions of inclusions are smaller
than the wavelength of incident radiation
and their volume fraction is not large,
one can calculate the effective refractive index of a composite particle
using a rule of the effective medium theory (EMT;
see, e.g., [7] for a review)
and then apply any light scattering method for homogeneous particles.
Applicability of scatterer models - example of astronomy.
For astronomical applications, the models of
homogeneous and core-mantle spheres (and infinite cylinders)
are primarily used. Models for homogeneous spheroids (and ellipsoids)
have been applied only seldomly.
Thus, the combined effects of shape and structure of cosmic dust grains
have barely been studied.
It should be added that
although inhomogeneous non-spherical aggregates were utilized
in a number of papers on cosmic dust modeling, very little attention
has been paid on these effects (see, e.g., [8]).
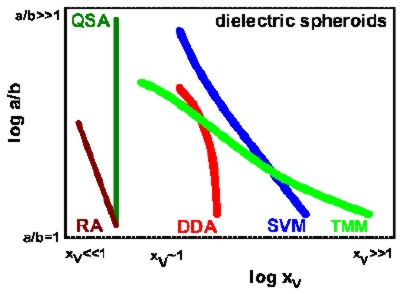 |
| Figure 1: Applicability ranges (domains left to the curves) of different methods in the case of dielectric prolate spheroids. Calculations were made with codes based on the Rayleigh (RA) and quasistatic (QSA) approximations, the discrete dipole (DDA), separation of variables (SVM) and extended boundary condition/T-matrix (TMM) methods. |
References:
- 1.
- Bohren, C.F. and Huffman, D.R. (1983) Absorption and Scattering of Light by Small Particles. Wiley, New York.
- 2.
- Mishchenko, M.I., Hovenier, J.W., and Travis, L.D. (2000) Light Scattering by Nonspherical Particles. Academic Press, San Diego.
- 3.
- Kruegel, E. (2003) Physics of Interstellar Dust. IOP.
- 4.
- Hovenier, J.W., Lumme, K., Mishchenko, M.I. et al. (1996) J. Quant. Spectr. Rad. Transf., 55, 695.
- 5.
- Wiscombe, W.J., and Mugnai, A. (1986) NASA Reference Publ., 1157, 1.
- 6.
- Lumme, K., and Rahola, J. (1998) J. Quant. Spectr. Rad. Transf., 60, 439.
- 7.
- Kolokolova, L., and Gustafson, B.A.S. (2001) J. Quant. Spectr. Rad. Transf., 70, 611.
- 8.
- Andersen, A.C. et al. (2002) Astron. Astrophys., 386, 296.
- 9.
- Farafonov, V.G., Il'in, V.B., and Prokopjeva, M.S. (2003) J. Quant. Spectr. Rad. Transf., in press.
- 10.
- Il'in, V.B., Voshchinnikov, N.V., Farafonov, V.G., Henning, Th., and Perelman, A.Ya. (2002) in G.Videen and M.Kocifaj (eds) Optics of Cosmic Dust. Kluwer, Dordrecht, p.71.
 To the top
To the top