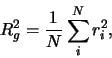Model realization and some results

The perceptron structure, on the basis of which the database is built, is defined by a number of the input and output parameters and a required accuracy. The number of input neurons corresponds to the number of parameters defining of the cluster properties: 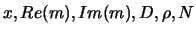$x, Re(m), Im(m), D, \rho, N$. The output perceptron data are the expansion coefficients of the scattering matrix elements in series of the generalized spherical functions.

The data for perceptron training was obtained using Mackowsky & Mishchenko code [3-4]. At 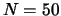$N=50$ the number of nonzero coefficients was equal to approximately 22-24. So, the number of output neurons was 30, and the number of "hidden" layers was 2 with 30 neurons in each layer.

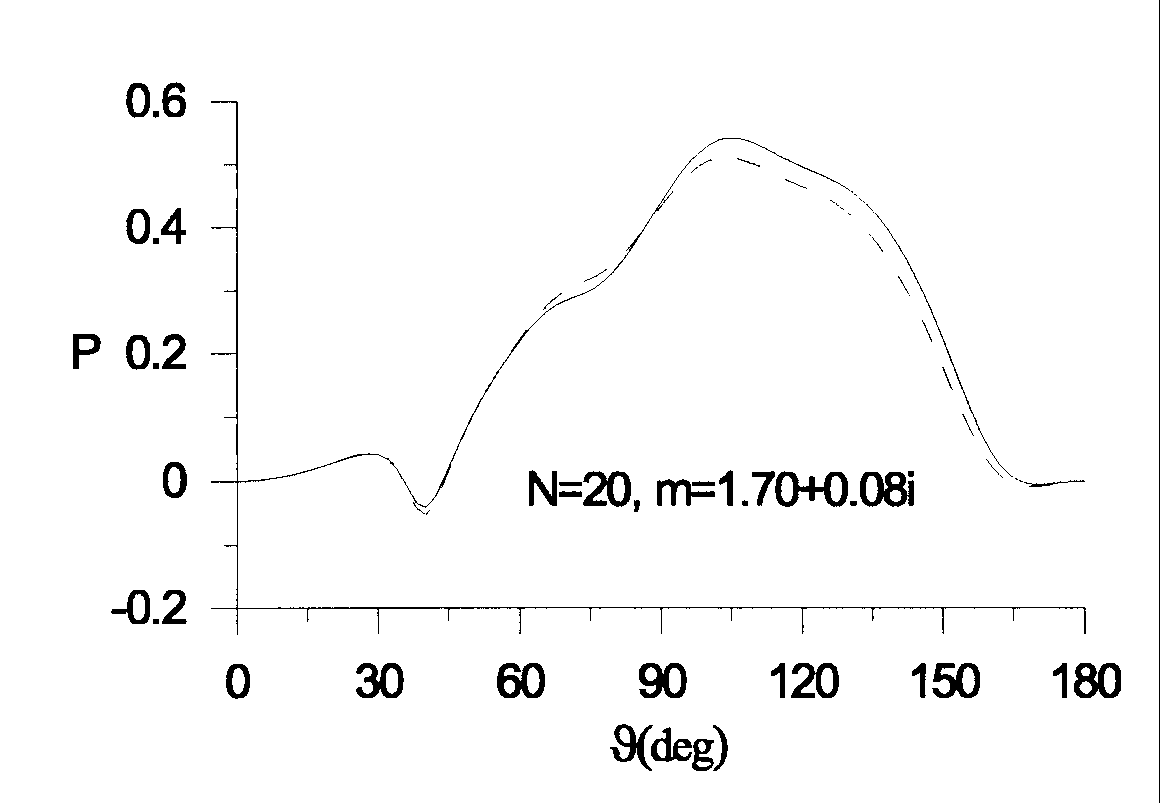
The generation algorithm for a fractal-like cluster of particles can be defined as follows:

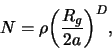$$N=\rho \biggl{(}\frac{R_g}{2a}\biggr{)}^D,$$ (1)

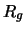where $R_g$ is the gyration radius of the cluster

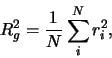$$R_g^2=\frac {1}{N} \sum_i^N{r_i^2},$$ (2)

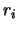and $r_i$ is the distance from the 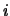$i$th particle to the center of mass of the cluster.

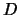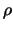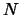Typical cluster structures with the same $D$, $\rho$ and $N$ but produced under different initial generation conditions are presented in Fig.1.

Figure 1: Typical clusters formed of 10 and 20 subparticles.

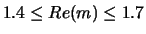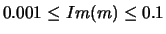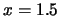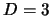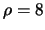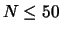Up to now, about two hundred points for the input parameters in the range of $1.4\leq Re(m) \leq 1.7$, $0.001\leq Im(m) \leq 0.1$, and for $x=1.5$, $D=3$, $\rho =8$ and $N\leq 50$ were utilized for training the perceptron. As the cluster structure depends on the generation conditions the expansion coefficients were averaged over 5--7 realizations of the clusters (for N < 35). During this training process the perceptron was defining and memorizing a hypersurface in space of input-output parameters that in the best way corresponded to the data set presented for training. The trained perceptron allows calculating the approximate values of the expansion coefficients for any input data from the data range that was used for the training.

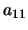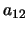Figure 2: Dependency of the $a_{11}$ and $a_{12}$ coefficients on 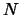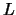$N$. $L$ is the coefficient number.

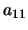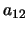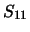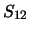Some examples of calculation of the dependencies of expansion coefficients $a_{11}$ and $a_{12}$ of the scattering matrixes elements $S_{11}$ and $S_{12}$ are given in Fig.2. The points correspond to the data obtained directly from the theory of light scattering by a cluster of spherical subparticles. Solid curves show data calculated by the perceptron.

Figure 3: Linear polarization degree 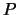$P$ vs the scattering angle 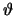$\vartheta$. Solid curve corresponds to the actual values, dotted line shows the values calculated by the perceptron.

In Fig.3 the linear polarization degrees of light scattered by clusters is presented. Note, that this refractive index (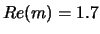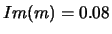$Re(m)=1.7$; $Im(m)=0.08$) was not used in perceptron training, which illustrates the potential of our database.

Advantages of the database are its small volume and quick access to the data. Moreover, there is a possibility to extend and make the database more precise without an increase of data time access and the volume of the database.

This research was supported by INTAS grant N 1999-00652.