On the optical characterization of media
(introductory notes)
Among the fundamental characteristics of a material/medium such as
chemical composition, density, conductivity, viscosity,
one should probably give the first place to the optical constants - the
refractive index ![]() and the extinction coefficient
and the extinction coefficient ![]() .
These quantities describe the interaction
of the electromagnetic radiation with a medium and well reacts to
variations of its composition and structure. Therefore, the optical
methods of measurements of
.
These quantities describe the interaction
of the electromagnetic radiation with a medium and well reacts to
variations of its composition and structure. Therefore, the optical
methods of measurements of ![]() and
and ![]() , having a high accuracy, speed,
and possibility of non-destructing and distant control, became
wide spread in practice of the physical/chemical analysis.
, having a high accuracy, speed,
and possibility of non-destructing and distant control, became
wide spread in practice of the physical/chemical analysis.
The optical characteristics are known to be in
particular sensitive to changes of the state of materials
in the regions of absorption bands. The position of spectral bands
is characterized by one of the following quantities: the frequency ![]() ,
the wavelength
,
the wavelength ![]() or the wavenumber
or the wavenumber
![]() .
Instead of the frequency
.
Instead of the frequency ![]() one can use also the circular frequency
one can use also the circular frequency
![]() .
.
In the physical optics one usually considers the electromagnetic radiation
in the wavelength interval from 1 nm to 1 mm. Generally,
there are the following range notation:
10-200 nm is called the vacuum ultraviolet (vacUV) spectral region,
that of 200-400 nm the ultraviolet (UV) one,
that of 400-800 nm the visual one,
that of 800 nm and further the infrared (IR) one.
In some regions radiation is often characterized by
the photon energy ![]() in units of electron-Volt (eV)
equal to the energy of an electron passed the potential
difference of one volt (1 eV = 8.0659
in units of electron-Volt (eV)
equal to the energy of an electron passed the potential
difference of one volt (1 eV = 8.0659 ![]() ).
).
The bands in the UV, visual and near IR regions are usually
connected with electron absorption, and those in the middle
and far IR regions with molecular and lattice absorptions.
Between the bands there are transparent regions where the values
of ![]() are usually close to 0.
are usually close to 0.
The electromagnetic radiation propagating in a medium is
characterazed by the amplitudes of the electric ![]() and
magnetic
and
magnetic ![]() vector oscillations, frequency, polarization state
and direction of propagation determined by the wavevector
vector oscillations, frequency, polarization state
and direction of propagation determined by the wavevector ![]() .
The expression for a monochromatic plane wave in an isotropic medium is
.
The expression for a monochromatic plane wave in an isotropic medium is
![\begin{displaymath}
\vec{E} = \vec{E}_0 \exp \left\{- 2 \pi {\rm i} f \left[t +...
...t(n+k{\rm i}\right) \frac{\vec{k}\vec{r}}{c} \right]\right\},
\end{displaymath}](img12.gif) |
(1) |
The parameter ![]() i in Eq.(1) describes the optical properties of
the medium where radiation propagates. The quantity
i in Eq.(1) describes the optical properties of
the medium where radiation propagates. The quantity ![]() is called
the complex refractive index, its real part
is called
the complex refractive index, its real part ![]() is equal to the ratio
of the velocity of electromagnetic radiation in vacuum to
the phase velocity of radiation in the medium, and its imaginary part
is equal to the ratio
of the velocity of electromagnetic radiation in vacuum to
the phase velocity of radiation in the medium, and its imaginary part ![]() characterizes the decrease of the radiation intensity in the medium
because of absorption.
characterizes the decrease of the radiation intensity in the medium
because of absorption.
The refractive index ![]() and the extinction coefficient
and the extinction coefficient ![]() of a medium are functions of
the frequency, and in the case of anisotropic media
of a medium are functions of
the frequency, and in the case of anisotropic media ![]() and
and ![]() also depend on the direction of radiation propagation
also depend on the direction of radiation propagation ![]() .
In the last case the values of
.
In the last case the values of ![]() and
and ![]() are tensors of the second order.
are tensors of the second order.
The intensity of radiation in a medium is proportional
to ![]() and its absorption is described by the Bouguer-Lambert-Beer law.
According to this law, the intensity of light
and its absorption is described by the Bouguer-Lambert-Beer law.
According to this law, the intensity of light ![]() after its propagation through a material slab of the thickness
after its propagation through a material slab of the thickness ![]() is connected with the initial intensity
is connected with the initial intensity ![]() as follows:
as follows:
| (2) |
The value
![]() being the ratio of the intensity
absorbed by the slab to the incident one is called the absorption
coefficient.
being the ratio of the intensity
absorbed by the slab to the incident one is called the absorption
coefficient.
From Eqs.(1)-(2) one obtains the expression for the absorption
coefficient
| (3) |
To characterize absorption by a medium, one also uses the quantity
![]() 100 (in percent) being the ratio of the intensityof the transmitted
radiation to that of the incident one and called
the transmission coefficient (or transmittance).
100 (in percent) being the ratio of the intensityof the transmitted
radiation to that of the incident one and called
the transmission coefficient (or transmittance).
For values of ![]() , to describe the optical properties
one often uses the quantity
, to describe the optical properties
one often uses the quantity
![]() called the
optical density.
called the
optical density.
The optical constants ![]() and
and ![]() allow one to estimate not only
transmittance and absorption of radiation, but also its reflection
at the border of two media. To calculate the reflection coefficient
(or reflectance) from the values of
allow one to estimate not only
transmittance and absorption of radiation, but also its reflection
at the border of two media. To calculate the reflection coefficient
(or reflectance) from the values of ![]() and
and ![]() for two bordering
media and the incidence angle
for two bordering
media and the incidence angle ![]() one can usitilize the Fresnel formula.
Note that the values of the transmission (
one can usitilize the Fresnel formula.
Note that the values of the transmission (![]() ), absorption (
), absorption (![]() ) and
reflection (
) and
reflection (![]() ) coefficients, which characterize the properties of a
sample, are connected
) coefficients, which characterize the properties of a
sample, are connected
| (4) |
In the electromagnetic theory one often uses not ![]() and
and ![]() , but
the dielectric functions (or permittivity) defined as
, but
the dielectric functions (or permittivity) defined as
![]() . As it follows from its definition,
. As it follows from its definition,
| (5) |
In an anisotropic medium, the permittivity is a symmetrical tensor and
can be transformed to the main axes
![\begin{displaymath}
\langle \varepsilon \rangle =
\begin{tabular}[c]{\vert ccc...
...on _b$\ & 0 \\
0 & 0 & $\varepsilon _c$\ \\
\end{tabular}
\end{displaymath}](img35.gif) |
(6) |
According to the optical properties, crystals are divided in 3 groups:
- cubic crystals when
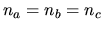 (these crystals
are optically isotropic);
(these crystals
are optically isotropic);
- single-axis crystals when
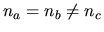 (these crystals
are trigonal, tetragonal and hexagonal. The direction
for which
(these crystals
are trigonal, tetragonal and hexagonal. The direction
for which 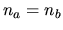 is called the optical axis. For a wave
propagating in this direction birefringence does not occur);
is called the optical axis. For a wave
propagating in this direction birefringence does not occur);
- biaxial crystals when
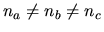 (these crystals
are monoclinic, triclinic and rhombic).
(these crystals
are monoclinic, triclinic and rhombic).
For single-axis crystals, the coinciding values of the refractive index are called the refractive index of the ordinary ray, the third principal refractive index is the principal refractive index of the extraordinary ray.
Like isotropic media, crystals are characterized not only by
the refractive indices, but also by the absorption indices that
can be combined in a tensor complex refractive index
| (7) |
The theory of interaction of light with a material that
accounts for the frequency dependence of the optical
functions
![]() was developed by Lorentz and Drude.
Despite the difference with the contemporary quantum-mechanical
approach, the results of this classical theory remain
formally valid and correctly describe the main features of the
process of interaction of radiation with a medium.
was developed by Lorentz and Drude.
Despite the difference with the contemporary quantum-mechanical
approach, the results of this classical theory remain
formally valid and correctly describe the main features of the
process of interaction of radiation with a medium.
A material medium in the classical theory is described by
a set of harmonic oscillators characterized by the eigenfrequency ![]() ,
the oscillator strength
,
the oscillator strength ![]() and the damping
and the damping ![]() . Using the
Maxwell equations for electromagnetic radiation and
the equations of the classical mechanics for description of
oscillator charge motion, one can obtain the expression for
the frequency dependence of the dielectric permittivity
. Using the
Maxwell equations for electromagnetic radiation and
the equations of the classical mechanics for description of
oscillator charge motion, one can obtain the expression for
the frequency dependence of the dielectric permittivity
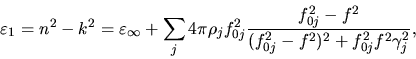 |
(8) |
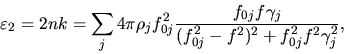 |
(9) |
Denoting the high-frequency dielectric permittivity by
![]() ,
the expression for
,
the expression for ![]() can written via
can written via ![]() and
and ![]() being the frequencies of the longitudal and transversal oscillations of
crystal lattice, respectively.
Taking into account the damping of the oscillations
(
being the frequencies of the longitudal and transversal oscillations of
crystal lattice, respectively.
Taking into account the damping of the oscillations
(
![]() and
and
![]() ), allowing one to
describe the anharmonicity, the dielectric permittivity is
), allowing one to
describe the anharmonicity, the dielectric permittivity is
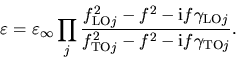 |
(10) |
For more information on the optical constant theory we refer the reader to the chapter of the classical C.F.Bohren & D.R.Huffman book [1] and a recent good textbook by M.Fox [2]. Some technical aspects of obtaing the optical constants are described briefly in another chapter of the book [1] and in more detail, e.g., in the books edited by E.D.Palik [3,4,5].
The optical constants for atmospheric aerosols are well presented in the HITRAN database (see http://www.hitran.com). Those for materials of astronomical interest are collected by us in the JPDOC database (http://www.astro.spbu.ru/JPDOC). This WWW database includes references to the papers where the optical constants were measured or calculated and original data obtained in the laboratory of the Friedrich Schiller University, Jena. A description of the JPDOC is given in [6,7].
(After V.M.Zolotarev)
References:
- 1.
- Bohren C.F., Huffman D.R. (1983) Absorption and Scattering of Light by Small Particles. J.Wiley & Sons, New York.
- 2.
- Fox M. (2001) Optical Properties of Solids. Oxford Univ. Press.
- 3.
- Palik E.D. (ed.) (1985) Handbook of Optical Constants of Solids. Academic Press, New York.
- 4.
- Palik E.D. (ed.) (1991) Handbook of Optical Constants of Solids, II. Academic Press, New York.
- 5.
- Palik E.D. (ed.) (1998) Handbook of Optical Constants of Solids, III. Academic Press, New York.
- 6.
- Henning Th., Il'in V.B., Krivova N.A., Michel B., and Voshchinnikov N.V. (1999) WWW database of optical constants for astronomy. Astron. Astrophys. Suppl. 136, 405.
- 7.
- Jaeger C., Il'in V.B., Henning Th., Mutschke H., Fabian D., Semenov D.A., and Voshchinnikov N.V. (2003) A database of optical constants of cosmic dust analogs. J. Quant. Spectrosc. Rad. Transf., in press.
 To the top
To the top