For particles of very large sizes, scattering can be considered as a result
of interference of the rays having multiple reflections and refractions
according
to the laws of geometrical optics. Diffraction at the particle edges
which gives a sharp maximum in the region of small angles can be
taken into account separately.
The formulation of general principles, computational schemes and
discussion of obtained results within the GO can be found in books
[7,11,124]. The papers [413,414] presented a method
where the scattering field was expressed via the field at the particle
surface using the Huygens-Kirchhoff principle, and
reflection and refraction laws were employed to find the unknown field
(the approach was called physical optics approximation).
Utilizing the GO method the author of [184] solved
the general question why the mean extinction cross-section for
an ensemble of large non-spherical particles
is always larger than this cross-section for equivolume spheres.
Illustrations of various applications of the method
are given in [28,30,155,192,263,412,425,427].
Note also a recent paper [242] where the GO method is applied
to analysis of light scattering by spheres with the size parameter 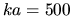 and the discovered theoretical and experimental relationships
in the oscillation of
and the discovered theoretical and experimental relationships
in the oscillation of 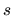 and and 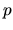 components of intensity
were used for successful solution of the inverse problem
of sizing. The accuracy of the GO method for non-spherical
particles was studied in a recent paper [332]
by comparison with the exact T-matrix method results. components of intensity
were used for successful solution of the inverse problem
of sizing. The accuracy of the GO method for non-spherical
particles was studied in a recent paper [332]
by comparison with the exact T-matrix method results.
|
 To the top
To the top