The main ideas of all the approximate methods are related to
certain regions of the values of the basic diffraction parameters -
the size parameter 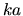 and the relative refractive index and the relative refractive index 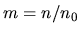 .
For instance, if .
For instance, if 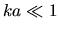 and and 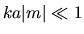 , one has the Rayleigh
scattering [418,419,421] when the particle can be interpreted
as an elementary dipole whose polarizability can be evaluate
from the electrostatic equations.
Apparently, Love [330] was first who paid attention to the fact that
the solution for a small sphere is identical to the Hertz oscillator.
The possibility to use the electrostatic approximation to calculate
the polarizability allows one to consider practically any shape scatterers -
from the regular ones (ellipsoid, cylinder, disc) [7,274]
to those with an arbitrary shape, structure and anisotropy
[308,309,313,405] (in the last case the polarizability tensor
should be found numerically) -
using the theory of the Rayleigh scattering. , one has the Rayleigh
scattering [418,419,421] when the particle can be interpreted
as an elementary dipole whose polarizability can be evaluate
from the electrostatic equations.
Apparently, Love [330] was first who paid attention to the fact that
the solution for a small sphere is identical to the Hertz oscillator.
The possibility to use the electrostatic approximation to calculate
the polarizability allows one to consider practically any shape scatterers -
from the regular ones (ellipsoid, cylinder, disc) [7,274]
to those with an arbitrary shape, structure and anisotropy
[308,309,313,405] (in the last case the polarizability tensor
should be found numerically) -
using the theory of the Rayleigh scattering.
The accuracy of the Rayleigh approximation for spheres was most carefully
investigated in [303].
Because of its simplicity this approximation was utilized in a huge number
of works to estimate the influence of the optical,
geometrical and morphological parameters of particles on their
scattering and extinction characteristics [7,11,25,124].
Typical examples are the papers on estimates of
the extinction spectra of disperse systems of small particles
[161,205,207,208,231,273,427,431].
The Rayleigh approximation is one of the main approaches in the theory
of light scattering by gases, liquids and solutions in the regions
distant from the critical points [18,26,130].
It should be noted that in the literature the terms including the
name of Rayleigh
(Rayleigh scattering, Rayleigh line, etc.) are often applied to quite
different physical phenomena.
We refer a reader to the paper of Yung [509]
where this question is discussed in detail.
In 1953 A.F. Stevenson in two papers [458,460] generalized
the Rayleigh theory, using the expansions of the fields in terms of
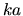 . For non-absorbing particles, the Rayleigh term is
proportional . For non-absorbing particles, the Rayleigh term is
proportional 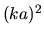 , and the next one found in the general case
by Stevenson is proportional to , and the next one found in the general case
by Stevenson is proportional to 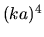 .
For some simple shapes (ellipsoid, thin disc, etc.)
one gets explicit, but rather complicated formules
(the generalization of the Stevenson theory for the case of
inhomogeneous particles and some simplifications see in [488]).
This theory is called in the literature the Rayleigh-Gans-Stevenson
approximation (RGS) keeping in mind the paper of R. Gans
on ellipsoids published in 1912 [224].
Note, however, that the principal questions of light
scattering by small spheroids were in our opinion considered
in the paper of Rayleigh [419].
Applications of the RGS theory to different light scattering problems
including orientation effects can be found in
[86, 94, 105, 235, 250, 251, 252, 376, 377, 409, 410, 459, 461]
(see also the review in [100]). .
For some simple shapes (ellipsoid, thin disc, etc.)
one gets explicit, but rather complicated formules
(the generalization of the Stevenson theory for the case of
inhomogeneous particles and some simplifications see in [488]).
This theory is called in the literature the Rayleigh-Gans-Stevenson
approximation (RGS) keeping in mind the paper of R. Gans
on ellipsoids published in 1912 [224].
Note, however, that the principal questions of light
scattering by small spheroids were in our opinion considered
in the paper of Rayleigh [419].
Applications of the RGS theory to different light scattering problems
including orientation effects can be found in
[86, 94, 105, 235, 250, 251, 252, 376, 377, 409, 410, 459, 461]
(see also the review in [100]).
|
 To the top
To the top