The T-matrix or transition matrix is well known in the quantum theory
of scattering [56] where one also uses the Heisenberg S-matrix connected
with the T-matrix by the relation
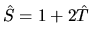 .
In contrast to the coordinate representation in the integral
equation method, where the scattered and incident fields are connected by
the Green function, the T-matrix connects the coefficients of the expansions
of the scattered and incident fields in terms of a complete
system of the vector basis functions. In the theory of light scattering
the T-matrix first appeared in the pioneer works of P.C. Waterman in 1965-1979
[496,497,498,499].
The initial formulation used the Huygens principle for perfectly
conducting [496] and dielectric [498] particles
was generalized in [497] where also
different ways of formulation of the method equations
without the Huygens principle and fictive sources were considered.
Although the papers of Waterman [496,497,498,499]
contained exhaustive information on principal and technical features of
the method, it attracted the attention of scientists in the optics
only after the publication of the paper of P.W. Barber and C. Yeh
in the Applied Optics in 1975 [147] where the method was formulated
using the Shelkunov equivalence theorems and called
the Extended Boundary Condition Method - EBCM.
Now both names are nearly equally used.
The further works of Barber's group
[142,143,144,145,146,227,324,328,493,494,508]
also had a noticeable influence on the growth of the method popularity.
The generalization of the T-matrix method for multi-particle configurations
were developed in [300,395,464], for multi-layered scatterers
in [300,396,493], and chiral particles of non-spherical shape in
[314,319].
For strongly aspherical weakly absorbing particles, the convergence
of the T-matrix method is rather weak, therefore
an iterative modification of the algorithm was suggested in [267] with
further development and applications in [266,268,269,316,318].
From the computational point of view, the method convergence problems
for strongly aspherical particles of large size are connected with the
errors of calculations of the integrals defining the T-matrix [49,60],
therefore a simple and effective way of solution of this problem is the
transition to representation of numbers in the computer with
extended accuracy
[359,361]. .
In contrast to the coordinate representation in the integral
equation method, where the scattered and incident fields are connected by
the Green function, the T-matrix connects the coefficients of the expansions
of the scattered and incident fields in terms of a complete
system of the vector basis functions. In the theory of light scattering
the T-matrix first appeared in the pioneer works of P.C. Waterman in 1965-1979
[496,497,498,499].
The initial formulation used the Huygens principle for perfectly
conducting [496] and dielectric [498] particles
was generalized in [497] where also
different ways of formulation of the method equations
without the Huygens principle and fictive sources were considered.
Although the papers of Waterman [496,497,498,499]
contained exhaustive information on principal and technical features of
the method, it attracted the attention of scientists in the optics
only after the publication of the paper of P.W. Barber and C. Yeh
in the Applied Optics in 1975 [147] where the method was formulated
using the Shelkunov equivalence theorems and called
the Extended Boundary Condition Method - EBCM.
Now both names are nearly equally used.
The further works of Barber's group
[142,143,144,145,146,227,324,328,493,494,508]
also had a noticeable influence on the growth of the method popularity.
The generalization of the T-matrix method for multi-particle configurations
were developed in [300,395,464], for multi-layered scatterers
in [300,396,493], and chiral particles of non-spherical shape in
[314,319].
For strongly aspherical weakly absorbing particles, the convergence
of the T-matrix method is rather weak, therefore
an iterative modification of the algorithm was suggested in [267] with
further development and applications in [266,268,269,316,318].
From the computational point of view, the method convergence problems
for strongly aspherical particles of large size are connected with the
errors of calculations of the integrals defining the T-matrix [49,60],
therefore a simple and effective way of solution of this problem is the
transition to representation of numbers in the computer with
extended accuracy
[359,361].
The analysis of the scattering characteristics of polydisperse ensembles
of particles with random orientation needs two additional integrations -
over size and orientation of scatterers and hence larger
computational resources. Therefore, very important is the derivation
of equations for the analytic orientational averaging
of all physically interesting optical characteristics:
the integral cross-sections and Mueller matrix
[54,98,281,345,350,348], the extinction matrix
of the transfer equation [344,348] and small-angle
scattering flux [57,388].
Using the apparatus of the quantum theory of angular momentum
we demonstrated that the equations for the orientational averaging of the
T-matrix and its bilinear forms (and hence the physically observer quantities)
do not depend on the particle nature and scattering waves [98,281].
In the works of M.I. Mishchenko [344]
and L.E. Paramonov [59,60] (see also the references in [60])
this approach was generalized for disperse systems with ordered orientation
of particles.
The numerical algorithms built on the equations of the
analytical orientational averaging were found to be the most
efficient ones for the analysis of light scattering characteristics of
ensembles of non-spherical particles with random orientation
(see the works of Mishchenko's group at the NASA Goddard Institute
for Space Studies [345,346,347,348,349,350,351,352,353,354,355,356,357,358,359,360,361,362]
and also the papers [47,48,49,60,63,64,78,102,103]
in Russian).
The important advantage of the T-matrix method is its natural
adaptation to the problems of the multi-scattering wave theory
[331,468,469,511,471,480,481,482,485,486,487],
radiative transfer equations [60,472,473],
scattering by cluster of particles [195,353,354,355,362],
particles of irregular shape [193] and
Chebyshev T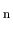 -particles [503],
Raman scattering [188],
extinction by polydisperse and polymorphic metal zoles
[102,103,282,283] and so on.
Thus, the T-matrix approach is practically universal for all
application fields of the light scattering theory.
Concluding the discussion of this method, we insistently refer
a reader to the reviews [362,483] where
the exhausted literature on the theory and
applications of the T-matrix method is collected. -particles [503],
Raman scattering [188],
extinction by polydisperse and polymorphic metal zoles
[102,103,282,283] and so on.
Thus, the T-matrix approach is practically universal for all
application fields of the light scattering theory.
Concluding the discussion of this method, we insistently refer
a reader to the reviews [362,483] where
the exhausted literature on the theory and
applications of the T-matrix method is collected.
|
 To the top
To the top